Luanxiao Zhao1*, Chenghao Cao2, Qiuliang Yao3,6, Yirong Wang1, Hui Li4, Hemin Yuan5, Jianhua Geng1, and De-hua Han6
1 State Key Laboratory of Marine Geology, Tongji University, Shanghai, China, 200092
2 Key Laboratory of Petroleum Resource Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, China, 100029
3 Halliburton Consulting and Project Management, Houston, USA, 77042
4 The school of electronic and information engineering, Xi'an Jiaotong University, Xi'an, China
5 Department of Geosciences and Natural Resource Management, University of Copenhagen, Copenhagen, Denmark
6 Department of Earth and Atmospheric Sciences, University of Houston, Houston, USA, 77004
Abstract:
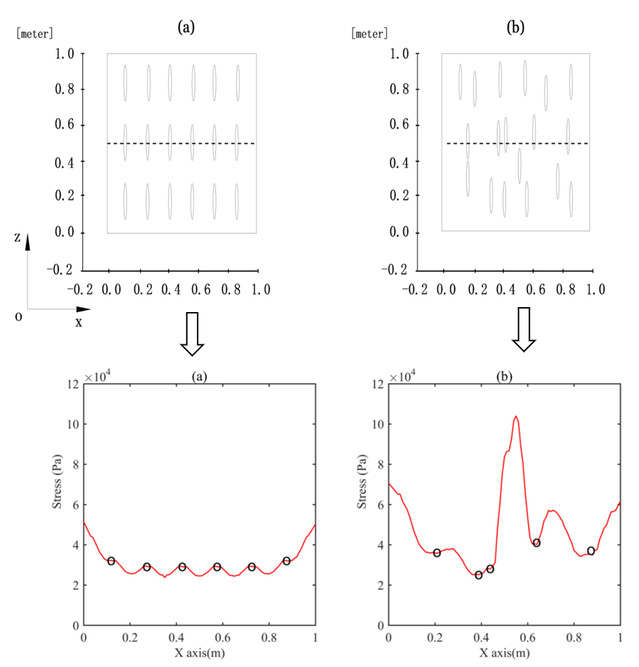
By evaluating the consistency of Gassmann theory with various inclusion-based effective medium theories, we investigate the impact of elastic interactions between ellipsoidal pores on the poroelasticity. To rule out any factors that can violate the Gassmann condition, other than elastic interactions, we construct idealized models that contain only single set of isolated, identical and vertically aligned ellipsoidal pores. The numerical simulation suggests that the periodic and random distribution of ellipsoidal pores can generate distinct pore pressure distributions. Then we analyze the precise conditions under which the various inclusion-based models are consistent with the underlying Gassmann relationship. The results reveal that: 1) Non-interacting effective medium theories are always consistent with the Gassmann prediction, simply because the elastic interactions are ignored; 2) The elastic interactions between randomly distributed pores causes heterogeneous pore pressure that violates the essential requirement of Gassmann theory. The differential effective medium (DEM) and self-consistent approximation (SCA) theories corresponding to this model thus are inconsistent with Gassmann prediction; 3) The elastic interactions between periodically distributed pores do not cause heterogeneous pore pressure therefore the Gassmann condition are fully satisfied. T-matrix approach explicitly takes into account such elastic interactions thus is consistent with Gassmann theory. It is interesting to notice that, on top of other well-known common type of heterogeneities, like pore structure heterogeneity or fluid heterogeneity, the distribution of pores and its associated elastic interactions can be a separate source of heterogeneity to generate non-uniform pore pressure as well as significant P- and S- wave dispersion.
Full article:https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2019JB018328